Toyota Venza: Fog Light Assembly

Toyota Venza Service Manual / Lighting (ext) / Fog Light Assembly

Components

COMPONENTS

ILLUSTRATION

Disassembly

DISASSEMBLY

PROCEDURE

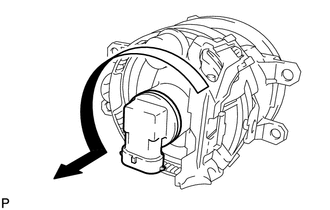
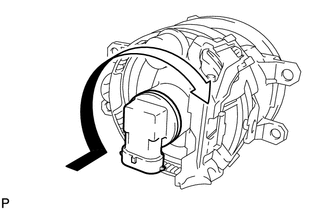
1. REMOVE FOG LIGHT BULB

(a) Turn the fog light bulb in the direction indicated by the arrow shown in the illustration and remove it.

NOTICE:

Do not touch the bulb glass.

Removal

REMOVAL

PROCEDURE

1. REMOVE FRONT BUMPER ASSEMBLY

(See page )

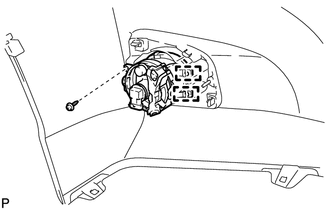
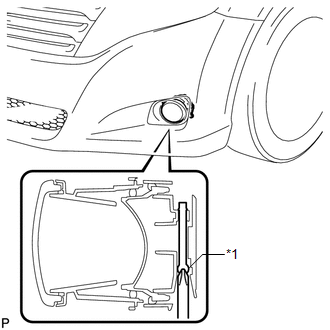
2. REMOVE FOG LIGHT ASSEMBLY

(a) Remove the screw.

(b) Disengage the 2 guides and remove the fog light assembly.

Adjustment

ADJUSTMENT

CAUTION / NOTICE / HINT

HINT:

It is possible that a bulb is incorrectly installed, affecting fog light aim. Bulb installation should be considered prior to performing the adjustment procedure.

PROCEDURE

1. PREPARE VEHICLE FOR FOG LIGHT AIM ADJUSTMENT

(a) Prepare the vehicle:

Ensure there is no damage or deformation to the body around the fog lights.
Fill the fuel tank.
Make sure that the oil is filled to the specified level.
Make sure that the coolant is filled to the specified level.
Inflate the tires to the appropriate pressure.
Unload the trunk and vehicle, ensuring that the spare tire, tools and jack are in their original positions.
Sit a person of average weight (68 kg, 150 lb) in the driver's seat.

2. PREPARE FOR FOG LIGHT AIMING

(a) Prepare the vehicle:

Place the vehicle in a location that is dark enough to clearly observe the cutoff line. The cutoff line is a distinct line, below which light from the fog lights can be observed and above which it cannot.
Place the vehicle at a 90° angle to the wall.
Create a 7.62 m (25 ft.) distance between the vehicle (fog light bulb center) and the wall.
Make sure that the vehicle is on a level surface.
Position the front wheels straight ahead.
Bounce the vehicle up and down to settle the suspension.
NOTICE:

A distance of 7.62 m (25 ft.) between the vehicle (fog light bulb center) and the wall is necessary for proper aim adjustment. If sufficient space is not available, secure a distance of exactly 3 m (9.84 ft.) to allow for checking and adjustment of fog light aim. (The size of the target zone will change with the distance, so follow the instructions in the illustration.)

(b) Prepare a piece of thick white paper (approximately 2 m (6.6 ft.) (height) x 4 m (13.1 ft.) (width)) to use as a screen.

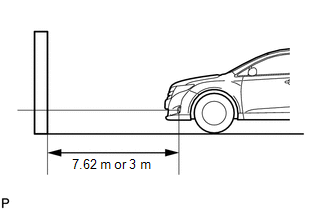
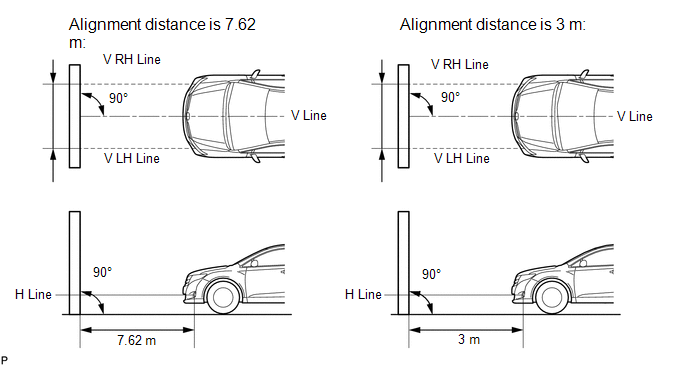
(d) Set the screen as shown in the illustration.

HINT:

Stand the screen perpendicular to the ground.
Align the V line on the screen with the center of the vehicle.

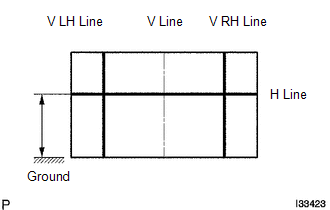
(e) Draw base lines (H, V LH, and V RH lines) on the screen as shown in the illustration.

HINT:

Mark the fog light bulb center marks on the screen. If the center mark cannot be observed on the fog light, use the center of the fog light bulb or the manufacturer's name marked on the fog light as the center mark.

(1) H Line (Fog light height):

Draw a horizontal line across the screen so that it passes through the center marks. The H line should be at the same height as the fog light bulb center marks of the fog lights.

(2) V LH Line, V RH Line (Center mark position of left-hand (LH) and right-hand (RH) fog lights):

Draw two vertical lines so that they intersect the H line at each center mark (aligned with the center of the fog light bulbs).

3. INSPECT FOG LIGHT AIMING

(a) Cover the fog light or disconnect the connector of the fog light on the opposite side to prevent light from the fog light that is not being inspected from affecting the fog light aiming inspection.

NOTICE:

Do not keep the fog light covered for more than 3 minutes. The fog light lens is made of synthetic resin, which may melt or be damaged due to excessive heat.

(b) Start the engine.

(c) Turn on the fog lights and check if the upper edge of the hot zone for each fog light matches the upper edge as shown in the illustration.

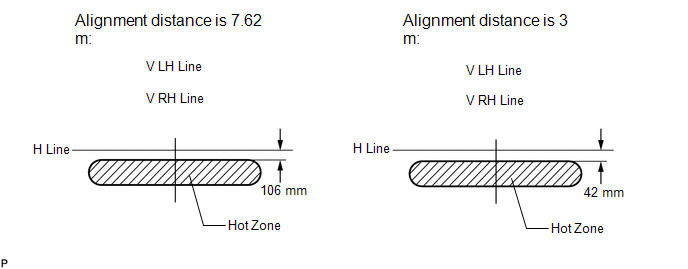
HINT:

If the alignment distance is 7.62 m (25 ft.):
The upper edge of the hot zone for the fog light should be 106 mm (4.19 in.) below the H line.
If the alignment distance is 3 m (9.84 ft.):
The upper edge of the hot zone for the fog light should be 42 mm (1.65 in.) below the H line.

4. ADJUST FOG LIGHT AIMING

(a) Adjust the aim vertically:

Adjust the aim of each fog light to the specified range by turning each aiming screw with a screwdriver.

Text in Illustration

*1	Aiming Screw

NOTICE:

The final turn of the aiming screw should be made in the clockwise direction. If the screw is tightened excessively, loosen it and then retighten it, so that the final turn of the screw is in the clockwise direction.

HINT:

If it is not possible to correctly adjust fog light aim, check bulb, fog light unit and fog light unit reflector installation.

Reassembly

REASSEMBLY

PROCEDURE

1. INSTALL FOG LIGHT BULB

(a) Turn the fog light bulb in the direction indicated by the arrow shown in the illustration to install it.

NOTICE:

Do not touch the bulb glass.

Installation

INSTALLATION

PROCEDURE

1. INSTALL FOG LIGHT ASSEMBLY

(a) Engage the 2 guides.

(b) Install the fog light assembly with the screw.

2. INSTALL FRONT BUMPER ASSEMBLY

(See page )

Door Mirror Foot Light

Components COMPONENTS ILLUSTRATION Removal REMOVAL CAUTION / NOTICE / HINT HINT: Use the same procedure for both the RH and LH sides. The procedure described below is for the ...

Hazard Warning Switch

...

Other materials about Toyota Venza:

Disassembly
DISASSEMBLY PROCEDURE 1. REMOVE GENERATOR PULLEY CAP (a) Using a screwdriver, puncture the center of the generator pulley cap and pry it off. NOTICE: Do not reuse the generator pulley cap. ...

Oxygen (A/F) Sensor Pumping Current Circuit / Open (Bank 1 Sensor 1) (P2237-P2239,P2252,P2253)
DESCRIPTION Refer to DTC P2195 (See page ). HINT: Although the DTC titles say oxygen sensor, these DTCs relate to the air fuel ratio sensor. DTC No. DTC Detection Condition Trouble Area P2237 ...

Inspection
INSPECTION PROCEDURE 1. INSPECT OUTER REAR VIEW MIRROR ASSEMBLY RH (a) Check the operation of the mirror surface. (1) Disconnect the outer rear view mirror assembly RH connector. (2) Apply battery ...